0ctf都过去这么久了,想来网上writeup已然到处都是,不过在这里还是简单记录一下自己比赛当时的解题过程吧……
首先这题给出了加解密的程序:
def encrypt(plaintext, key):
ciphertext = ""
for i in xrange(len(plaintext)):
p = ord(plaintext[i]) - ord('a')
k = ord(key[i % len(key)]) - ord('a')
c = (tr[k][p] + i**7) % 26
ciphertext += chr(c + ord('a'))
return ciphertext
def decrypt(ciphertext, key):
plaintext = ""
for i in xrange(len(ciphertext)):
c = ord(ciphertext[i]) - ord('a')
k = ord(key[i % len(key)]) - ord('a')
p = tr[k][(c - i**7) % 26]
plaintext += chr(p + ord('a'))
return plaintext
初看程序会觉得有种好神奇的感觉的说,竟然用了同一个矩阵同时做加解密的置换,只能说矩阵是特殊设计好的了,本来还以为加解密的key值可能不同,观察一下矩阵却发现其实加解密的key应该是一样的,因为矩阵每一行逆过来都是自身。不过,这都是废话,下面开始正式解题:
首先,i**7很明显是多余的部分,于是上来就将i**7从密文中减掉,这样密文每个字母就和明文字母一一对应了,此时,整个程序其实就和维吉尼亚密码很相似了,唯一的区别就是维吉尼亚密码中采取的是偏移量不同的恺撒密码,而这里采取的是26种置换(也就是表中对应的26行)。
于是乎,果断祭出之前破维吉尼亚密码的程序,破维吉尼亚密码的时候,首先是对重合指数进行分析,确定密钥长度,这一步显然对于这题的加密算法也是适用的。然后确定密钥长度后,就是尝试用每一个密钥解密,统计解密出来的字母频率与标准频率的差值,显然我们这里也可以这样,只是需要把解密过程替换下,将凯撒加密替换成这里的置换表。
本来这样很轻松就解决了这题的,结果可曾想,竟然在改程序的时候犯了超二的错,结果一直过不掉,甚至开始怀疑他这里故意破坏了频率:
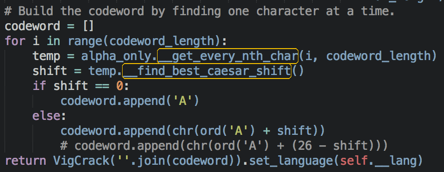
如上图所示,它这个程序本身是调用的Caesar的encipher来做的解密,由于凯撒加密和解密的区别只是密钥而已,所以他这里是可以的,也正是这样,他下面得到密钥的时候就要用26来减,也就是注释的那句,结果刚开始我忘记改这里了,于是乎就真的就是满满的都是泪……
这题不得不说挺水的,浪费这么多时间不得不说是个悲剧,最后给出比赛时改的代码。